[이론]
회귀분석
- 상관분석을 통해 두 변수 간에 의미있는 선형성이 있음을 알았지만 인과관계를 설명하는건 아니었음->회귀분석으로 인과관계 확인
- 마케팅 비용 늘리면 매출 늘어나는가?얼마나 늘어나?
- 회귀분석은 관찰된 연속형 변수들에 대해 변수들 사이의 모형을 구한 뒤, 적합도를 측정해내는 분석 방법
- 예측함수의 형태에 따라 선형회귀/비선형회귀
- 독립변수의 개수에 따라 단순회귀/다중회귀
- 종속변수의 개수에 따라 단변량회귀/다변량회귀
- 선형 회귀분석의 목적
- 설명 : 종속변수에 대한 설명변수(독립변수)의 영향을 측정, 설명함
- 예측 : 설명변수(독립변수)정보가 있을 때 이에 따른 종속 변수를 예측함
단순 선형 회귀분석


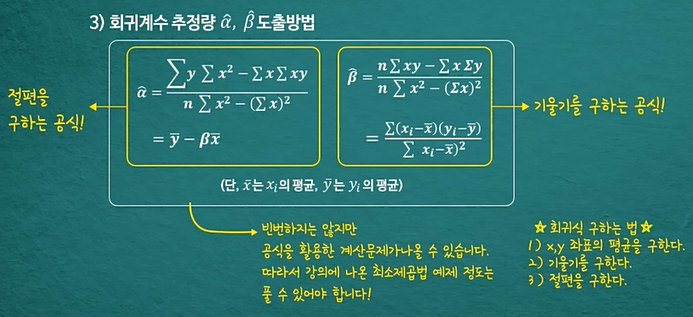
회귀분석의 가설
1) 회귀식이 존재하는지?
-> f검정을 통해 회귀식의 존재여부 판정
* 선형 회귀분석의 가설
- 귀무가설 : x변수들은 y변수와 선형관계 없음(기울기=0)
- 대립가설 : x변수들은 y변수와 선형관계 있음(기울기!=0)
2) 기울기가 있다면. 만약에 독립변수 x가 하나가 아니라면 각각의 독립변수 x가 얼마나 영향을 끼치는지
->t검정
선형회귀분석의 4가지 가정(선형성,정규성,등분산성,독립성)
정규,등분산,독립에 대한 가정은 오차에 대한 가정
잔차 : 내가 만든 모델과 실제 관측값의 차이
오차 : 진짜 회귀선과 실제 관측값의 차이
선형회귀분석3_통계파트(변수처리,성능평가)
다른 이슈가 있는 데이터일 때
* 이상치
대응방법
- 데이터 변환
- Robust Regression
- 잔차의 제곱 대신 절대값의 합이 최소가 되도록 계수 추정
- Quantile Regression
- 구간별로 다른 회귀식을 사용. 한 구간에서는 이상치였지만 이상치가 속해있는 구간에 속해있는 회귀식을 사용하면 이상치가 아님
* 다중공선성
독립변수 간에 강한 상관관계가 있는 경우
* 회귀모델의 유의성 검정
- f검정통계량에 대한 확률(p-value)
- 회귀식이 종속변수 y의 변량을 설명하는가?
* 회귀변수의 유의성 검정
- 각 독립변수의 t검정통계량에 대한 확률(p-value)
- 해당 독립변수가 종속변수 y의 변량을 설명하는가?
* 선형회귀모델 평가
회귀분석모델이 얼마나 인과관계를 잘 표현하고 있지?
-> R^2(결정계수, coefficient of determination)
- 변수간 영향을 주는 정도 또는 인과 관계의 정도를 정량화해서 나타낸 수치
- 추정한 선형의 모형이 주어진 자료에 대해 얼마나 적합한가를 나타냄
- 0≤R^2 ≤1. 1에 가까울수록 인과관계가 높음
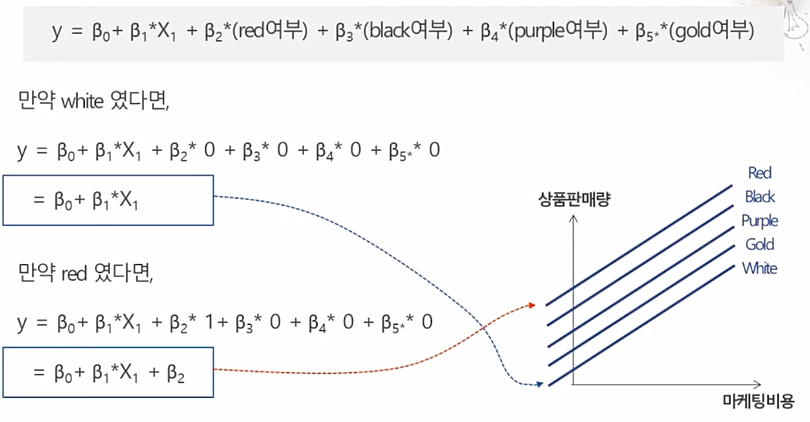
one-hot-encoding
범주형 데이터를 수치형 데이터로 변환.
단어 집합의 크기를 벡터의 차원으로 하고, 표현하고 싶은 단어의 인덱스에 1의 값을 부여하고, 다른 인덱스에는 0을 부여하는 단어의 벡터 표현 방식

가변수(Dummy Variable) - 범주형 자료를 0과 1로 표현
- 해당 범주형 변수의 기준값을 정함(drop_first 또는 drop_last와 같은 방법으로 정하기도함)
- 그 값을 제외한 나머지 범주형값을 새로운 열이름으로 하여 열 추가

sklearn - LinearRegression()
- 선형회귀분석함수
- LinearRegression()함수 내 fit_intercept로 절편 적합 여부 설정 가능
- LinearRegression()함수의 fit() 메서드에 학습 데이터 할당 가능
- 모델 객체의 coef_와 intercept_어트리뷰트로 각각 계수와 절편 확인 가능
- 모델 객체의 predict()메서드로 예측
sklearn - mean_absolute_error()
- MAE연산을 위한 함수
sklearn - mean_squared_error()
- MSE연산을 위한 함수
- 제곱근연산까지 하면 RMSE 계산 가능
train test split 하는 이유.
전체 데이터를 학습하지 않고 데이터를 나눠 학습하는 이유는 모델이 과적합되는 것을 막고 머신러닝 알고리즘의 성능을 평가하기 위해서.
실제로 모델을 활용하기 위해서는 학습에 사용되지 않은 데이터에 대한 예측을 잘 해야함
주어진 데이터에만 치중하여 학습하면 조금이라도 다른 패턴을 가진 데이터에 대해서는 모델의 성능이 떨어짐
fit() : 훈련해라. 데이터 학습시키는 메서드. 머신러닝이 데이터셋에 머신러닝 모델을 맞추는것
'Data > Python' 카테고리의 다른 글
| [Data/Python] 로지스틱 회귀분석 (0) | 2024.01.25 |
|---|---|
| [Data/Python] 비계층적 군집분석 (1) | 2024.01.25 |
| [Data/Python] 상관분석 (0) | 2024.01.24 |
| [Data/Python] 이론 정리 (1) | 2024.01.24 |
| [Data/Python]실습_데이터 전처리: 결측치 이상치 (0) | 2024.01.17 |


