Signal
- 어떠한 정보를 담고 있는 독립변수에 관한 함수
- signal로 표현된 데이터를 컴퓨터로 처리하고자 함
System
- signal을 받아들여 처리하고 signal을 내보냄

Audio Signals
- 시간(t)에 관한 함수
Image Signals
- 공간좌표(x, y)에 관한 함수
- 빛의 밝기 구분 -> 흑백영상
- 2차원 평면에서 픽셀좌표
- x, y가 크면 빛의 세기가 크다는 뜻. 흰색에 가까워짐
Color images
- r(x, y), g(x, y), b(x, y)
- 세개의 독립된 영상이 쌓이면 컬러 이미지
- 빨간색 이미지는 R의 빛의 세기가 크다는 의미
Video Signals
- 공간, 시간에 관한 함수
- r(x, y, t), g(x, y, t), b(x, y, t)
- ex) input signal로 깜빡이는 동영상을 System안에 넣었을 때 output으로 안, 밖이 잘 보이는 동영상이 나옴
Analog Signal Processing vs Digital Signal Processing
- Analog signal processing
- 반도체에서 주로 사용

- Digital signal processing

A/D Converter : Analog Signal을 Digital Signal로 변환
D/A Converter : Digital Signal을 Analog Signal로 변환
DSP의 장점
- 용이성.정확성.저장하기에 쉬움.비용이 적게 듬
- Analog signal의 정확도를 계속 유지하기엔 cost가 많이 듬
Continuous-Time vs Discrete-Time Signals

Analog-to-Digital Conversion
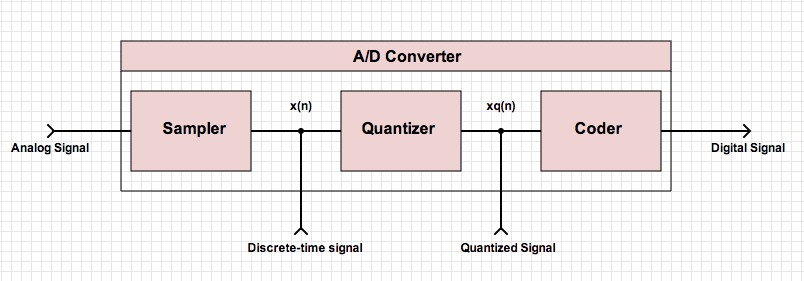
- analog signal -> digital signal 과 continuous -> discrete은 다른 얘기임
* analog signal -> digital signal 변환 방법
1) Sampling
2) Quantization
discrete의 의미
- time domain에서 discrete
- 각 value domain에서 discrete
1) Sampling
time domain에서 continuous signal을 discrete signal로 변환해야함

- sampling frequency(Fs) : discrete signal을 만들기 위해 continuous signal에서 얻어진 단위시간(주로 초) 당 sampling 횟수. 단위는 Hz(역수 초 1/s)
1Hz sampling : 1초에 한 번씩 sampling
2Hz sampling : 1초에 두 번씩 sampling
- sampling 주기가 짧을 수록(= sampling frequency가 높을 수록) 원래의 신호를 더 잘 복원함.

2) Quantization
- 각 value domain에서 discrete

(a)처럼 value domain이 continuous한 상태에서 (b)처럼 value domain이 discrete한 상태로 만들기 위해 강제로 실제 값을 approximating함
참고
'DSP' 카테고리의 다른 글
| [DSP] Sinusoids (0) | 2024.03.11 |
|---|
